I’m trying a new blog format. I’m going to lay these out light science experiments in high school: hypothesis/experiment/results/discussion. We’ll see how it goes.

The notebook for this project can be found here

Hypothesis

Introduction

Wassenstein generative adversarial networks minimize the EM-distance between a generated distribution, and a true distribution:

 EM(P(generated data), P(actual data))

A conditional GAN allows one to include a condition (as an input to the generator), that effects the generated data:

 EM(P(generated data|y), P(real data|y))

Hypothesis

I want to see if I can include the y condition by simply forcing it to be a particular value. The WGAN critic simply the EM distance between the generated data and the real distribution, so by including y in the data, I convert the minimization objective to

 EM(P(generated data, y), P(real data, y))

In effect, I’ve taken away the generator’s ability to control the condition. At the same time, I pass the condition in to the generator, so that it is forced to adapt to the y passed to it. The critic sees the joint distribution of data and condition, so it learns the full joint distribution.

Method

This is quite easy, and for my experiment I’ve used data from one of 10 2d Gaussians. Here’s the real data-distribution, colored by y, the conditional:

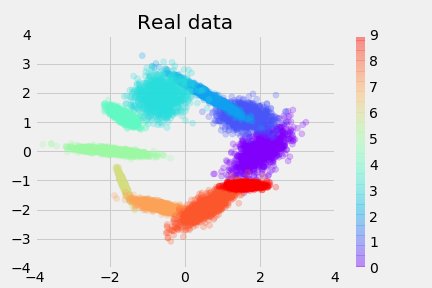
The generator’s structure is simply:

Gen (
   (layers): ModuleList (
     (0): Linear (32 -> 128)
     (1): ReLU ()
     (2): Linear (128 -> 256)
     (3): ReLU ()
     (4): Linear (256 -> 256)
     (5): ReLU ()
     (6): Linear (256 -> 2)
   )
 )

The critic is:

Critic (
  (layers): ModuleList (
    (0): Linear (12 -> 256) # 2 inputs from the generator, and 10 one-hot classes.
    (1): ReLU ()
    (2): Linear (256 -> 256)
    (3): ReLU ()
    (4): Dropout (p = 0.5)
    (5): Linear (256 -> 256)
    (6): ReLU ()
    (7): Dropout (p = 0.5)
    (8): Linear (256 -> 1)
  )
)

I use the improved Wasserstien training regularization method, rather than the clipping approach.

During each training step I do the following:

  1. Train the critic (x5)
    1. Sample a batch from the dataset, of both x and matching ys.
    2. Sample from the generator, passing in y
    3. Review the sample with the critic, passing in y and the sample.
    4. Review the real data with the critic, passing in y and x.
    5. Compute the loss, as mean(sample_review) - mean(real_review) + improved wasserstein regularization term.
    6. Optimize the critic
  2. Sample a batch from the dataset, of both x and matching ys.
  3. Sample from the generator, passing in y
  4. Review the sample with the critic, passing in y and the sample.
  5. Review the real data with the critic, passing in y and x.
  6. Compute the loss, as mean(sample_review)
  7. Optimize the generator

The notebook for this project can be found here

Results

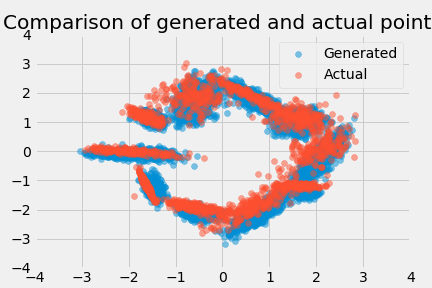
This worked great! By the 30-thousandth iteration, the generator was closely matching both the clusters:

And the classes of the data:

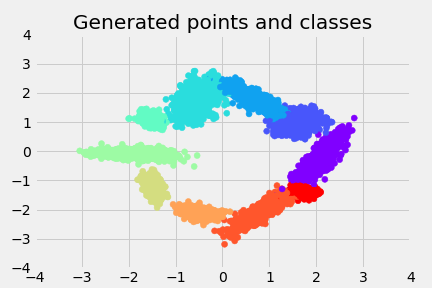
This means I now have a way to feed in conditions to a WGAN, and really easily generate data conditioned on it.

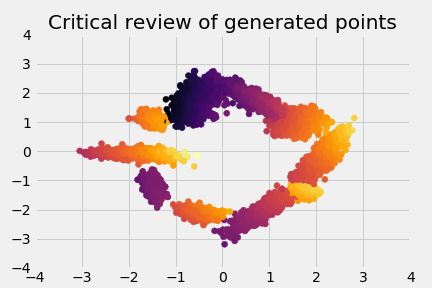
It’s also interesting to look at the scores of the generated points, so these are the “reviews” of the data:

Discussion

This leaves a few open questions:

  1. Is it possible to double-down and make a generative process for ys. In this case we drew samples of y from the dataset, but perhaps it would be better to generate both data and y values, but generate y values in a separate module so that later I can set conditions.
  2. Does it work for MNIST? And CIFAR?
  3. Is it possible to condition on continuous values? This is easy to test as a complex multiple regression problem.

Conclusion

It’s quite easy to make a conditional-WGAN, by simply:

  1. Passing the conditions to the data-generator.
  2. Also passing the conditions (and the generated data) to the critic when scoring fake data.
  3. Passing the real-data and matching conditions to the critic when scoring real data.